- Susun digit ke dalam kotak:4 | 2 | 9Masing-masing angka dari 429 ditempatkan dalam kotak terpisah.
Cara Menghitung Pembagian Bersusun dengan Metode Garis Pak Trisno

Mengajarkan penjumlahan dan pengurangan mungkin terasa mudah bagi beberapa orang karena banyak cara untuk memvisualisasikannya. Tetapi, menjadi tantangan tersendiri bagi Mama ketika si Kecil sudah melangkah ke materi matematika selanjutnya, yaitu perkalian dan pembagian. Jika si Kecil belum hafal kelipatan bilangan, mereka akan lebih susah dalam membagi bilangan yang jumlahnya banyak, seperti ratusan atau ribuan.
Apalagi, kadang anak diam saja ketika mereka tidak mengerti materi matematika di kelas, sehingga mereka membawa kebingungan itu di rumah, menunggu Mama mengajarkan. Mama mungkin memerlukan banyak metode untuk menyesuaikan dengan tingkat pemahaman si Kecil.
Jangan khawatir, Ma, seorang guru matematika sekaligus youtuber bernama Trisno MathNian mengajarkan salah satu metode yang menarik lewat kanalnya, yaitu dengan metode pembagian garis ala Pak Trisno. Metode ini menggunakan kotak-kotak berjajar secara vertikal dan efektif digunakan untuk mempermudah pembagian bersusun, terutama untuk siswa SD, dengan pembagian digit demi digit sambil membawa sisa ke kotak sebelahnya.
Maksudnya seperti apa, sih? Nah, di artikel berikut, Popmama.com akan mencoba menjelaskan pembagian angka dengan metode garis a la Pak Trisno. Simak dengan baik, yuk!
1. Contoh pertama → 429 ÷ 3
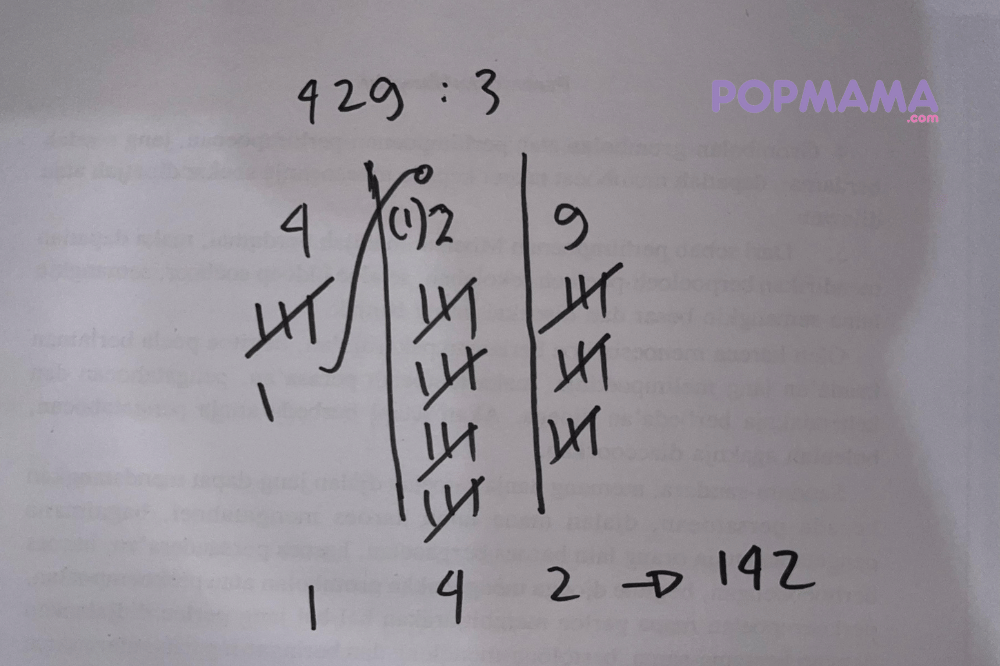
Jika kita ingin menghitung: 429 ÷ 3, maka langkah-langkahnya sebagai berikut:
- Bagi digit pertama (4 ÷ 3):
- 3 masuk ke 4 1 kali, sisa 1
- Tulis 1 di bawah kotak pertama
- Sisa 1 ini dioper ke kotak kedua, jadi sekarang isinya 12 (gabungan sisa 1 dan angka 2)4 | 2 | 9↓ ↓ ↓1 | |
- Bagi isi kotak kedua (12 ÷ 3):
- 3 masuk ke 12 4 kali, sisa 0
- Tulis 4 di bawah kotak kedua
- Tidak ada sisa, jadi kotak ketiga tetap 94 | 2 | 9↓ ↓ ↓1 | 4 |
- Bagi isi kotak ketiga (9 ÷ 3):
- 3 masuk ke 9 3 kali, sisa 0
- Tulis 3 di bawah kotak ketiga4 | 2 | 9↓ ↓ ↓1 | 4 | 3
- Rapatkan hasilnyaSetelah digabung, hasilnya 429 ÷ 3 = 143
2. Contoh kedua → 872 ÷ 4
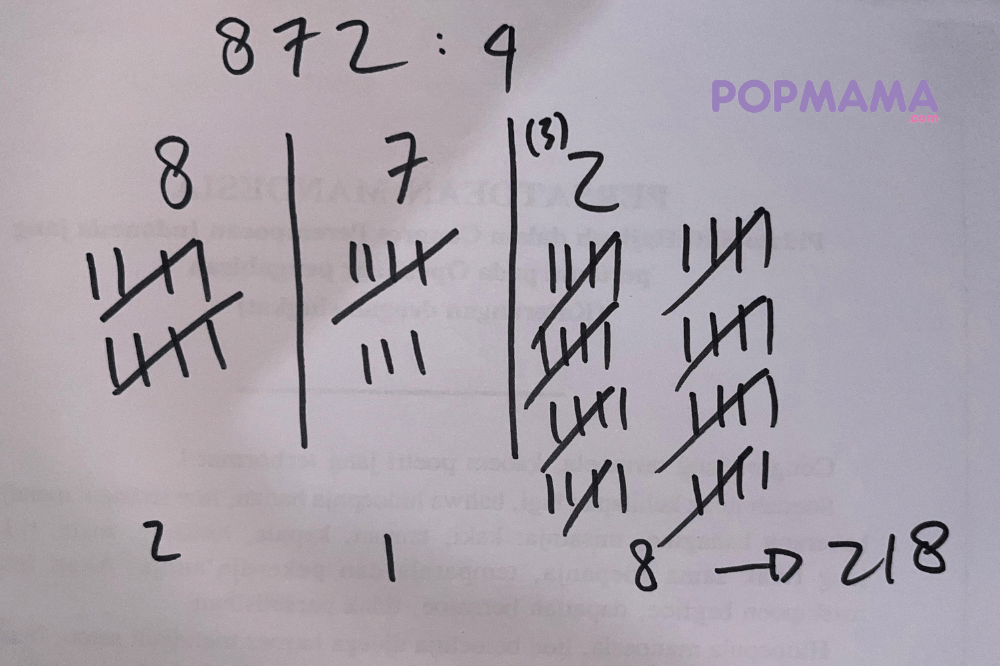
Jika ingin menghitung 872:4, maka langkah-langkahnya sebagai berikut:
- Tuliskan setiap digit dalam kotak:8 | 7 | 2
- Jumlah kotak pertama → 8 ÷ 4
- 4 masuk ke 8 2 kali, sisa 0
- Tulis 2 di bawah kotak pertama
- Tidak ada sisa → lanjut8 | 7 | 2↓ ↓ ↓2 | |
- Jumlah kotak kedua → 7 ÷ 4
- 4 masuk ke 7 1 kali, sisa 3
- Tulis 1 di bawah kotak kedua
- Sisa 3 dioper ke kotak berikut → jadi 328 | 7 | 2↓ ↓ ↓2 | 1 |
- Jumlah kotak ketiga → 32 ÷ 4
- 4 masuk ke 32 8 kali, sisa 0
- Tulis 8 di bawah kotak ketiga8 | 7 | 2↓ ↓ ↓2 | 1 | 8
- Gabungkan angka. Akan mendapat jawaban → 872 ÷ 4 = 218
Apakah Bisa Dipakai untuk Perkalian Juga?

Secara konsep tidak langsung cocok, karena metode garis/kotak ini berbasis pada pembagian digit demi digit dari kiri, sedangkan perkalian itu justru menggabungkan/mengalikan, dan hasilnya bisa melibatkan lebih banyak digit.
Namun, ada metode cukup mirip yang disebut Perkalian Metode Lattice / Kotak Silang (Metode Jepang)
Misalnya, kita memiliki angka → 23 × 4
Untuk mengerjakan dengan metode ini, langkah-langkahnya adalah sebagai berikut:
- Buat kotak 2 kolom (karena 23 punya dua digit)
- Kalikan satu per satu:
- 2 × 4 = 8
- 3 × 4 = 12
- Susun hasilnya seperti ini:
- Puluhan dari 2×4 → 08
- Puluhan dari 3×4 → 12
- Tambahkan sesuai posisi: 2 | 3× | 4----------- 08 | 12
- Gabungkan hasilnya menjadi → 92
Namun, perlu diketahui bahwa cara ini tidak umum digunakan, karena perkalian itu menjumlahkan hasil kali, sementara metode kotak itu bekerja bagus untuk pecah digit (pembagian atau desimal).
Lalu, Metode Pak Trisno Cocok untuk Apa Saja?

1. Pembagian bilangan besar (terutama oleh 1 digit)
Dengan metode Pak Trisno, anak-anak bisa lebih mudah mengaplikasikan alur logika “bagi satu digit → bawa sisa → lanjut” secara visual.
- Contohnya → 3.624 ÷ 6 . Maka setiap digit ditempatkan dalam kotak, dibagi satu per satu dari kiri ke kanan.
2. Pembagian desimal
Metode ini bisa dikembangkan untuk membantu anak paham tempat nilai desimal saat membagi.
- Contohnya → 4,5 ÷ 3 . Maka di kotak kedua (setelah koma), tetap diberi nilai dan hasil desimal ditaruh di atas koma juga.
3. Konversi pecahan ke desimal (via pembagian)
Misalnya untuk menghitung 7 ÷ 4 → bisa disusun dalam metode kotak untuk hasil desimal bertahap (1,75).
4. Operasi campuran (pembagian + sisa)
Metode ini sangat membantu untuk memperlihatkan bagaimana “sisa” bisa muncul dan “dibawa” ke angka selanjutnya.
Misalnya untuk menghitung → 245 ÷ 2. Jika metode ini dipakai, maka hasilnya 122 sisa 1. Dari sini bisa terlihat jelas saat pembagian angka terakhir tidak habis.
5. Pemahaman nilai tempat
Karena dalam metode ini, angka ditulis dalam kotak per digit, siswa juga jadi terbantu dalam memahami bahwa → 429 itu = 400 + 20 + 9 . Masing-masing angka memiliki kedudukan tempat yang berbeda. Ada yang satuan, puluhan, dan ratusan.
Nah, Ma, itu dia penjelasan mengenai pembagian angka dengan metode garis a la Pak Trisno. Mudah dimengerti, bukan? Coba Mama praktikkan dengan contoh bilangan yang lain, ya!